Do bacteria mutate randomly, or do they mutate for a purpose? Researchers have been puzzling over this conundrum for over a century.
In 1943, microbiologist Salvador Luria and physicist turned biologist Max Delbrück invented an experiment to argue that bacteria mutated aimlessly. Using their test, other scientists showed that bacteria could acquire resistance to antibiotics they hadn't encountered before.
The Luria–Delbrück experiment has had a significant effect on science. The findings helped Luria and Delbruck win the Nobel Prize in physiology or medicine in 1969, and students today learn this experiment in biology classrooms. I have been studying this experiment in my work as a biostatistician for over 20 years.
Decades later, this experiment offers lessons still relevant today, because it implies that bacteria can develop resistance to antibiotics that haven't been developed yet.
Bacteriophages are viruses that specifically infect bacteria.
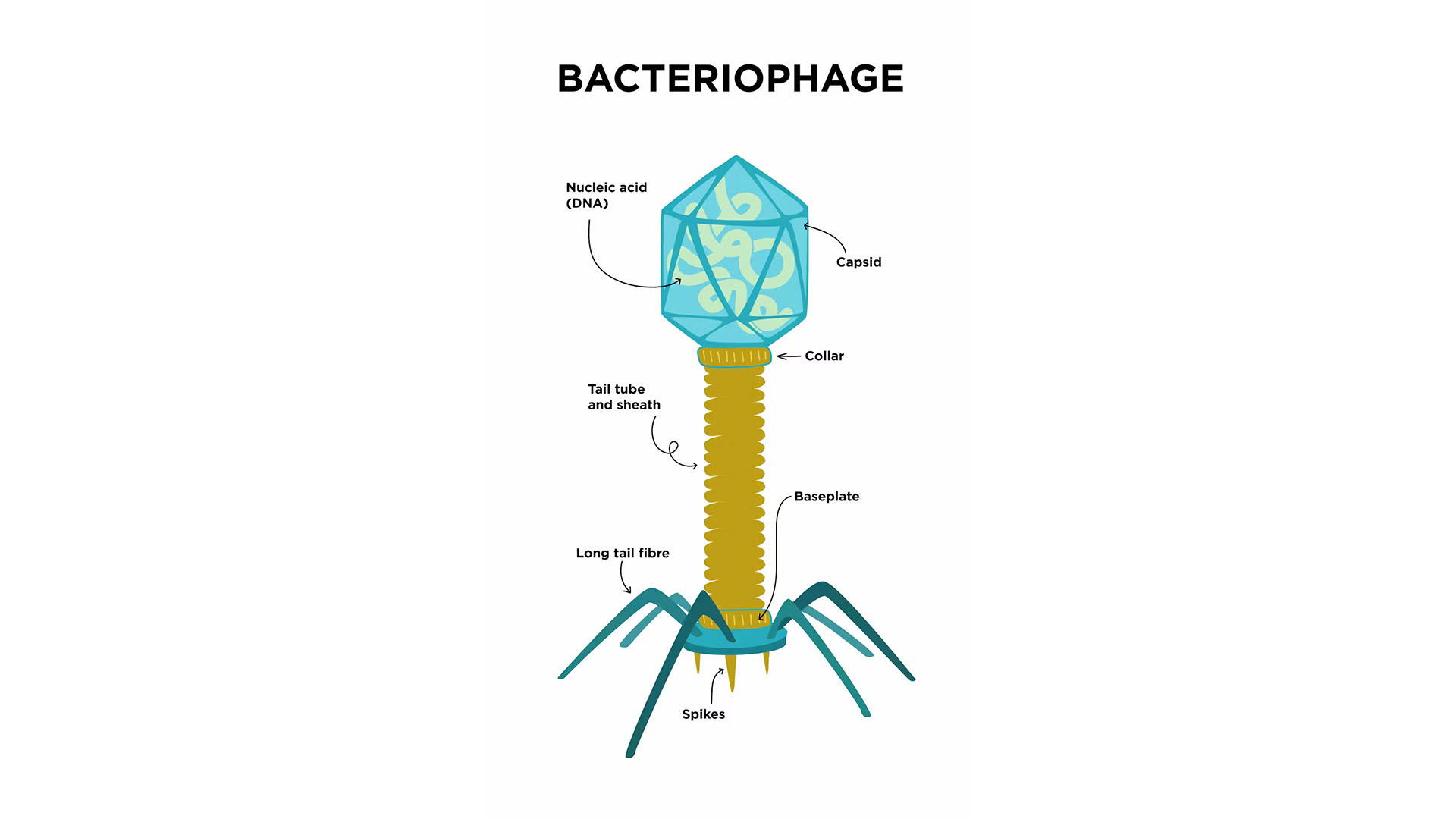
Slot machines and a eureka moment
Imagine a test tube containing bacteria living in nutrient broth. The broth is cloudy due to the high concentration of bacteria within it. Adding a virus that infects bacteria, also known as a phage, into the tube kills most of the bacteria and makes the broth clear.
However, keeping the test tube under conditions favorable for bacterial growth will turn the broth cloudy again over time. This indicates that the bacteria developed resistance against the phages and were able to proliferate.
What role did the phages play in this change?
Get the world’s most fascinating discoveries delivered straight to your inbox.
Some scientists thought the phages incited the bacteria to mutate for survival. Others suggested that bacteria routinely mutate randomly, and the development of phage-resistant variants was simply a lucky outcome. Luria and Delbrück had been working together for months to solve this conundrum, but none of their experiments had been successful.
On the night of Jan. 16, 1943, Luria got a hint about how to crack the mystery while watching a colleague hit the jackpot at a slot machine. The next morning, he hurried to his lab.
Luria's experiment consisted of a few tubes and dishes. Each tube contained nutrient broth that would help the bacteria E. coli multiply, while each dish contained material coated with phages. A few bacteria were placed into each tube and given two opportunities to generate phage-resistant variants. They could either mutate in the tubes in the absence of phages, or they could mutate in the dishes in the presence of phages.
This diagram of the Luria-Delbrück experiment depicts colonies of phage-resistant variants of E. coli (red) developing in petri dishes.
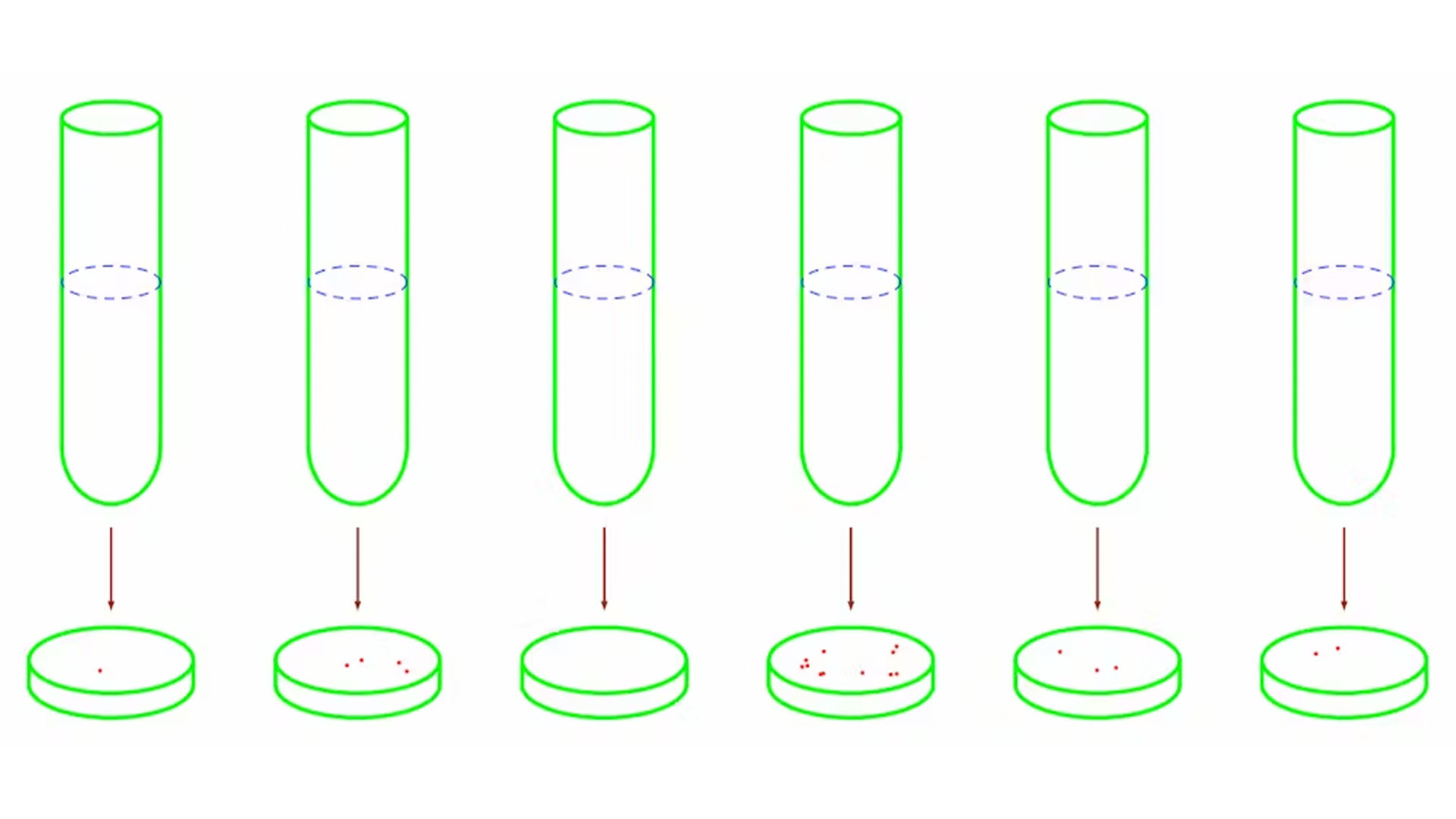
The next day, Luria transferred the bacteria in each tube into a dish filled with phages. The day after that, he counted the number of resistant bacterial colonies in each dish.
If bacteria develop resistance against phages by interacting with them, none of the bacteria in the tubes should have mutations. On the other hand, only a few of the bacteria — say, 1 out of 10 million bacteria — should spawn resistant variants when they are transferred into a dish containing phages. Each phage-resistant variant would grow into a colony, but the remaining bacteria would die from infection.
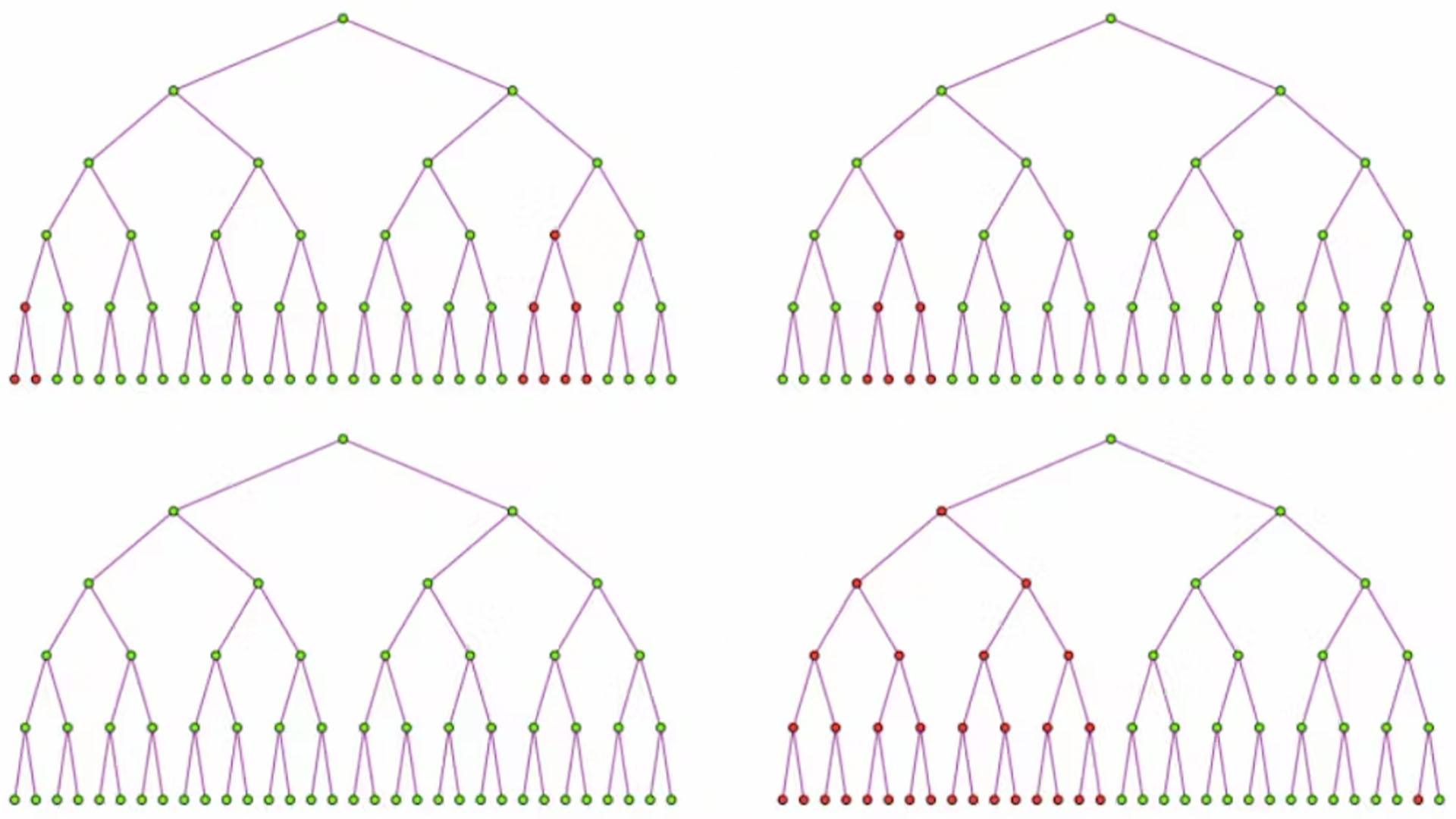
If bacteria develop resistance independently of interacting with phages, some of the bacteria in the tubes will have mutations. This is because each time a bacterium divides in a tube, it has a small probability of spawning a resistant variant. If the starting generation of bacteria is the first to mutate, at least half of the bacteria will be resistant in later generations. If a bacterium in the second generation is the first to mutate, at lest an eighth of the bacteria will be resistant in later generations.
Like small-prize cash-outs in slot machines, late-generation mutations occur more often but give fewer resistant variants. Like jackpots, early-generation mutations occur rarely but give large numbers of variants. Early-generation mutations are rare because early on there are only a small number of bacteria available to mutate.
For example, in a 20-generation experiment, a mutation occurring at the 10th generation of bacteria would give 1,024 phage-resistant variants. A mutation occurring at the 17th generation would give only four phage-resistant variants.
The number of resistant colonies in Luria's experiments showed a similar pattern to that of slot machine cash-outs. Most dishes contained no or small numbers of mutant colonies, but several contained a large number of mutant colonies that Luria considered jackpots. This meant that the bacteria developed resistant variants before they interacted with the phages in the dishes.
An experiment's legacy
Luria sent a note to Delbrück after his experiment was completed, asking him to check his work. The two scientists then worked together to write a classic paper describing the experimental protocol and a theoretical framework to measure bacterial mutation rates.
Mutations that confer resistance against phages (red) early on will spawn a large number of phage-resistant variants, while mutations that occur later on will spawn only a few resistant variants.
Other scientists conducted similar experiments by replacing phages with penicillin and with tuberculosis drugs. Similarly, they found that bacteria did not need to encounter an antibiotic to acquire resistance to it.
RELATED STORIES
Bacteria have relied on random mutations to cope with harsh, constantly changing environments for millions of years. Their incessant, random mutations will lead them to inevitably develop variants that are resistant to the antibiotics of the future.
Drug resistance is a reality of life we will have to accept and continue to fight against.
This edited article is republished from The Conversation under a Creative Commons license. Read the original article.
I began researching into the Luria–Delbrück distribution in 1998 at the suggestion of a renowned statistical distribution expert. The Luria–Delbrück distribution is a family of related distributions describing the probabilistic behavior of the numbers of mutants observed in a Luria–Delbrück experiment, which is also called the fluctuation experiment. The Luria–Delbrück distribution plays a key role in allowing microbiologists to extract information on microbial mutation rates from mutant count data generated by fluctuation experiments. I have devised an array of computational methods for the analysis of data generated by fluctuation experiments. I also made a computer package and a Web tool to help biologists analyze data from fluctuation experiments. My research results have appeared in mathematics, statistics and biology journals. My second research interest is in statistical education for public health students.