Infamous 'sofa problem' that boggled mathematicians for decades may finally have a solution
A math problem delineating the largest-size sofa that can fit around a corner has finally been solved, though it may not help you move.
Twenty-five years too late to help Ross get his new couch into his apartment in "Friends," a mathematician has finally solved the pesky "sofa problem."
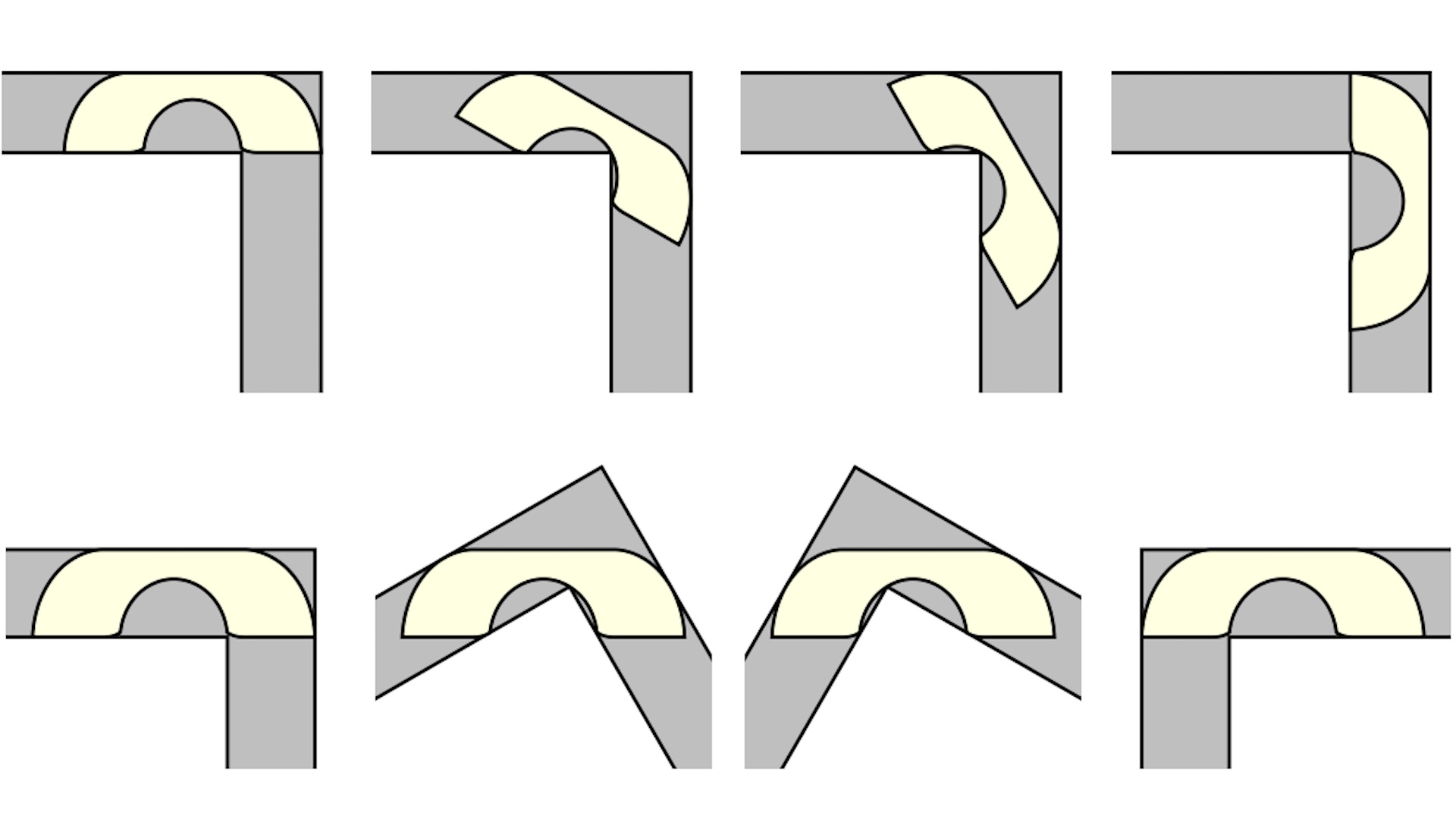
The math problem delineates the largest-size sofa that can fit around a corner of a given width — exactly the problem faced by the characters in an episode of "Friends" that aired in 1999. Ross' pleas of "Pivot!" could have been avoided, it turns out, if he'd only considered a Gerver's sofa with 18 curve sections and a maximum area of 2.2195 units. (Okay, so maybe it wouldn't have been that helpful.)
The solution to the sofa problem is a first for mathematics. The problem was posited by Austrian-Canadian mathematician Leo Moser in 1966. Moser asked for the largest possible area of a single shape in one plane that could move around a right-angled corner of a hallway with a unit width of one. While this might seem simple, the math is quite complicated, as the problem involves both area maximization and movement of the shape.
Now, Jineon Baek, a postdoctoral researcher in mathematics at Yonsei University in South Korea, has arrived at an answer. Baek posted his solution on Dec. 2 on the preprint website ArXiv. In just over 100 pages of mathematical proofs, Baek found that for a hallway with a width of 1 unit, the imaginary sofa's maximum area can be 2.2195 units — narrowing the answer down with precision from the previously known range of between 2.2195 and 2.37 units. The proof has not yet been published in a peer-reviewed journal and will need to be worked through by other mathematicians to determine that it is, indeed, optimal.
The "Gerver" of Gerver's sofa is mathematician Joseph Gerver, an emeritus professor at Rutgers University who posited the lower bound of 2.2195 in 1992. But there had been debate over whether the sofa could be larger, with a team in 2018 using a computer-assisted proof to suggest that 2.37 was actually the upper bound.
Gerver's sofa is a broad U-shaped couch with a curved "seat" that can squeeze around the corner without getting hung up. The question was whether this painstakingly designed sofa — made of 18 separate curves put together — was really the largest, most optimal shape that could make the turn. Baek worked through the geometry of the shape and its movement and found that Gerver's solution was, in fact, correct.
Get the world’s most fascinating discoveries delivered straight to your inbox.
The proof created a ripple of interest on social media.
"This is the optimal sofa," user @morallawwithin wrote on the social platform X on Dec. 6, posting a picture of the rather wide-armed sofa shape. "You may not like it, but this is what peak optimization looks like."

Stephanie Pappas is a contributing writer for Live Science, covering topics ranging from geoscience to archaeology to the human brain and behavior. She was previously a senior writer for Live Science but is now a freelancer based in Denver, Colorado, and regularly contributes to Scientific American and The Monitor, the monthly magazine of the American Psychological Association. Stephanie received a bachelor's degree in psychology from the University of South Carolina and a graduate certificate in science communication from the University of California, Santa Cruz.


